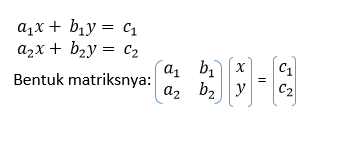Matriks dan
Pengaplikasian pada Penyelesaian SPL
Pendahuluan
Matriks merupakan kumpulan
bilangan, simbol atau ekspresi berbentuk persegi panjang yang disusun menurut
baris dan kolom.
M
= baris
N = kolom
Cth :
- · Diagonal utama dan sekunder pada matriks
Di
dalam materi mengenai matriks juga dikenal istilah diagonal. Ada dua jenis
diagonal di dalam matriks yaitu diagonal utama dan diagonal sekunder. Diagonal
utama merupakan garis miring
yang ditarik dari sisi kiri atas matriks menuju
sisi kanan bawah matriks. Sementara diagonal sekunder adalah kebalikannya.
Seperti bisa dilihat pada gambar berikut:
Jenis – jenis matriks
berdasarkan banyaknya baris dan kolom
1.
Matriks persegi
Matriks yang memiliki jumlah baris dan kolom
yang sama, misalnya 4x4, 2x2, atau
5x5. Sehingga ordonya dilambangkan n x n.
5x5. Sehingga ordonya dilambangkan n x n.
2.
Matriks
baris
Adalah matriks yang hanya memiliki satu buah
baris namun memiliki beberapa kolom. Matriks ini ordonya adalah 1 x n dimana n harus lebih besar dari 1.
Contohnya 1 x 2, 1 x 4, 1 x 6, dsb.
3.
Matriks
kolom
Merupakan kebalikan
dari matriks baris. Hanya terdiri dari satu kolom namun memiliki beberapa
baris. Ordo dari matriks ini adalah n x 1 dimana n harus
lebih besar dari 1. Contohnya adalah 2 x 1, 3 x 1, 5 x 1, dsb.
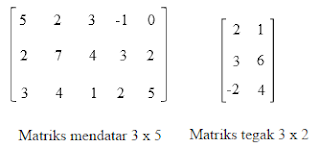
4. Matriks mendatar
Adalah matriks yang memiliki jumlah kolom yang lebih banyak
dibandingkan jumlah barisnya. Contohnya adalah 3 x 5, 4 x 6, dsb.
5. Matriks tegak
Merupakan kebalikan dari matriks mendatar dimana jumlah
barisnya lebih banyak dibandingkan jumlah kolomnya. Contohnya adalah 6 x 3, 4 x
2, 8 x 5, dsb.
- Jenis matriks berdasarkan pada pola elemennya1 Matriks nol
1. Matriks nol
Merupakan matriks dengan ordo m x n dimana seluruh elemennya memiliki
nilai nol.
2 2. Matriks Diagonal
Merupakan matriks persegi yang elemennya
bernilai nol kecuali pada diagonal utamanya.
3 3. Matriks Identitas
Matriks
Identitas adalah matriks yang anggota pada diagonal utamanya selalu 1
4. Matriks segitiga atas
Adalah
matriks yang keseluruhan nilai dibawah diagonal utamanya adalah nol.
2 5. Matriks
segitiga bawah
Merupakan
kebalikan dari matriks segitiga atas dimana seluruh elemen yang ada di atas diagonal utamanya bernilai nol.
3 6. Matriks
simetris
Merupakan
sebuah matriks dimana elemen yang ada di atas dan dibawah doagonal utamanya memiliki susunan nilai yang sama.
4 7. Matriks
skalar
Adalah
matriks yang memiliki elemen diagonal utama bernilai sama sementara elemen yang
lain nilainya adalah nol.
1 8. Matriks transpose
Matriks
transpose merupakan matriks yang mengalami pertukaran elemen dari kolom menjadi
baris atau sebaliknya.
Contoh:
9. Determinan suatu matriks
Untuk menentukan determinan dari suatu
matriks dapat digunakan beberapa cara:
1.
Matriks berordo 2x2
2. Metode
sarrus
3. Metode
ekspansi baris dan kolom
10. Matriks Singular
Matriks
Singular yaitu matriks yang nilai determinannya 0.
Contoh:
11. Invers Matriks
sifat-sifat dari invers suatu matriks:
operasi matriks invers:
12. Operasi dasar matriks:
Pengaplikasian Matriks
·
Mengubah SPL menjadi matriks
Kita bisa menggunakan matriks untuk
menyelesaikan persoalan SPL,
Pertama-tama kita ubah dahulu SPL nya
menjadi bentuk persamaan matriks, setelah itu baru menerapkan konsep matriks
yaitu invers dan determinan.
Sistem
persamaan dua variabel x dan y:
Sistem
persamaan tiga variabel x, y, dan z:
Ø
Penerapan invers pada SPL
Kita
menerapkan sifat invers yaitu:
Contoh:
1)
Tentukan nilai x dan y yang memenuhi Sistem Persamaan Linier (SPL)
dengan menggunakan konsep invers matriks
Penyelesaian:
1.
Ubah
dahulu SPL menjadi persamaan matriks
2.
Menentukan matriks B
Jadi, solusi dari Sistem Persamaan Linear
(SPL) nya adalah, x = 1 dan y = -1
Ø
Penerapan determinan pada SPL
Metode ini sering kali disebut sebagai
metode ‘Cramer’
Sistem persamaan dua variabel x dan y
contoh:
1.
Tentukan nilai x dan y yang memenughi
sistem persamaan linear (SPL) dengan menggunakan konsep determinan matriks
(cara cramer).
Jadi,
solusi dari Sistem Persamaan Linear (SPL) nya adalah, x = 1 dan y = -1.